El radio de convergencia de una serie de la forma 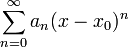 , con
, con 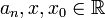 , viene dado por la expresión:
, viene dado por la expresión:
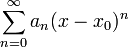 , con
, con 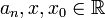 , viene dado por la expresión:
, viene dado por la expresión:
Si nos limitamos al conjunto de los números reales, una serie de la forma 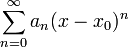 , con
, con 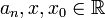 , recibe el nombre de serie de potencias centrada en
, recibe el nombre de serie de potencias centrada en 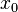 . La serie converge absolutamente para un conjunto de valores de
. La serie converge absolutamente para un conjunto de valores de  que verifica que
que verifica que 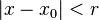 , donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de
, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de  pertenecientes al intervalo
pertenecientes al intervalo 
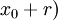 ,
ya que la convergencia para los extremos de este ha de estudiarse
aparte, por lo que el intervalo real de convergencia puede ser también
semiabierto o cerrado. Si la serie converge solo para
,
ya que la convergencia para los extremos de este ha de estudiarse
aparte, por lo que el intervalo real de convergencia puede ser también
semiabierto o cerrado. Si la serie converge solo para 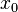 ,
, 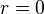 . Si lo hace para cualquier valor de
. Si lo hace para cualquier valor de  ,
, 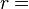

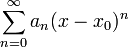 , con
, con 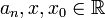 , recibe el nombre de serie de potencias centrada en
, recibe el nombre de serie de potencias centrada en 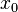 . La serie converge absolutamente para un conjunto de valores de
. La serie converge absolutamente para un conjunto de valores de  que verifica que
que verifica que 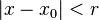 , donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de
, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de  pertenecientes al intervalo
pertenecientes al intervalo 
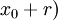 ,
ya que la convergencia para los extremos de este ha de estudiarse
aparte, por lo que el intervalo real de convergencia puede ser también
semiabierto o cerrado. Si la serie converge solo para
,
ya que la convergencia para los extremos de este ha de estudiarse
aparte, por lo que el intervalo real de convergencia puede ser también
semiabierto o cerrado. Si la serie converge solo para 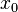 ,
, 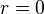 . Si lo hace para cualquier valor de
. Si lo hace para cualquier valor de  ,
, 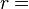

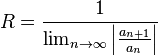
No hay comentarios:
Publicar un comentario