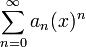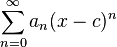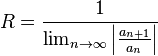martes, 10 de julio de 2012
Unidad 4
Nombre de la asignatura: Cálculo Integral
Carrera: Ingeniería en Sistemas Computacionales
Clave de la asignatura: ACF-0902
(Créditos) SATCA: 3 - 2 - 5
Temario Unidad 4
TEMA: SERIES
4.1 Definición de serie.
4.1.1 Finita.
4.1.2 Infinita.
4.2 Serie numérica y convergencia Prueba de la razón (criterio de D´Alembert) y Prueba de la raíz (criterio de Cauchy).
4.3 Serie de potencias.
4.4 Radio de convergencia.
4.5 Serie de Taylor.
4.6 Representación de funciones mediante la serie de Taylor.
4.7 Cálculo de Integrales de funciones expresadas como serie de Taylor.
4.1 Definición de serie
Una serie es la suma indicada de los terminos de una sucesión.
Así, de las sucesiones anteriores obtenemos las series
1+4+9+16+25
Cuando el numero de terminos es limitado, se dice que la sucesion o serie es finita. Cuando el numero de terminos es ilimitado, la sucesición o serie se llama una sucesión infinita o una serie infinita.
El termino general o termino enesimo es una expresion que indica la ley de la fomación de los terminos
Ejemplo :
Así, de las sucesiones anteriores obtenemos las series
1+4+9+16+25
Cuando el numero de terminos es limitado, se dice que la sucesion o serie es finita. Cuando el numero de terminos es ilimitado, la sucesición o serie se llama una sucesión infinita o una serie infinita.
El termino general o termino enesimo es una expresion que indica la ley de la fomación de los terminos
Ejemplo :
En la primera sucesión anterior, el termino general o termino enesimo es n2. El
primer terminose obtiene haciendo n=1, el decimo termino haciendo n=10

El estudio de las series consiste en la evaluación de la suma de un número finito n de términos sucesivos, y mediante un pasaje al límite identificar el comportamiento de la serie a medida que n crece indefinidamente.

En matemáticas, una serie es la generalización de la noción de suma a los términos de una sucesión infinita. Informalmente, es el resultado de sumar los términos: a1 + a2 + a3 + · · lo cual suele escribirse en forma más compacta con el símbolo de sumatorio:
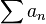 .
.
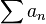 .
.El estudio de las series consiste en la evaluación de la suma de un número finito n de términos sucesivos, y mediante un pasaje al límite identificar el comportamiento de la serie a medida que n crece indefinidamente.
Una secuencia o cadena «finita», tiene un primer y último término bien definidos; en cambio en una serie infinita,
cada uno de los términos suele obtenerse a partir de una determinada
regla o fórmula, o por algún algoritmo. Al tener infinitos términos,
esta noción suele expresarse como serie infinita, pero a diferencia de las sumas finitas, las series infinitas requieren de herramientas del análisis matemático para ser debidamente comprendidas y manipuladas.
Existe una gran cantidad de métodos para determinar la naturaleza de convergencia o no-convergencia de las series matemáticas, sin realizar explícitamente los cálculos.
Existe una gran cantidad de métodos para determinar la naturaleza de convergencia o no-convergencia de las series matemáticas, sin realizar explícitamente los cálculos.
4.1.1 Finita.
Una
serie numerica es un conjunto especial de números que se forma
ordenadamente siguiendo determinada ley o condición, así por ejemplo.
2, 4, 6, 8, 10, 12, 14
2, 4, 8, 16, 32, 64,....
1, 1/2, 1/3, 1/4, 1/5
3, 6, 10, 12, 14, 20
xi = 0 para todo i > n y yi = 0 para todo i > m. En este caso el producto de
xi = 0 para todo i > n y yi = 0 para todo i > m.
En este caso el producto de Cauchy de  y
y  se verifica es
se verifica es  .
.
 y
y  se verifica es
se verifica es  .
.
Por lo tanto, para series finitas (que son sumas finitas), la
multiplicación de Cauchy es directamente la multiplicación de las
series.
4.1.2 Infinita.
Es un arrglo ordenado de numeros reales, uno para cada entero positivo. Mas formal mente una sucesión infinita es una funcion cuyo dominio es el conjunto de enteros positivos y cuyo rango es un conjunto de numeros reales. Podemos indicar una sucesion mediante a1 ,a2 ,a3,...., simplemete por {an}
Se puede especificar una sucesion dando suficientes terminos iniciales para establecer un patron como en
1, 4, 7, 10, 13, ....
mediante una formula explicita para el n-énesimo termino, como en
an = 3n-2, n ≥ 1
Para alguna  , sea
, sea  y
y  . Entonces
. Entonces
 , sea
, sea  y
y  . Entonces
. Entoncespor definición y la fórmula binomial. Dado que, formalmente,
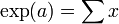 y
y  , se ha demostrado que
, se ha demostrado que  . Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series, se ha demostrado por lo tanto la fórmula exp(a + b) = exp(a)exp(b) para todo
. Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series, se ha demostrado por lo tanto la fórmula exp(a + b) = exp(a)exp(b) para todo  .
.4.2 Serie numérica y convergencia Prueba de la razón (criterio de D´Alembert) y Prueba de la raíz (criterio de Cauchy).
Carácter de una serie.
- Convergente: Cuando la suma es un número real.
- Divergente: Cuando la suma da + o - infinito.
- Oscilante: Cuando no es ninguna de las anteriores.
Convergencia de series con solo términos positivos
- Teorema 1: Toda serie de términos positivos es convergente o divergente, pero nunca oscilante.
- Teorema 2: Alterando arbitrariamente el orden de los términos, descomponiendo arbitrariamente cada uno de los sumandos, no se altera el carácter de la serie, ni varía su suma.
- Si k < 1 la serie converge (Fin)
- Si k > 1 la serie diverge (Fin)
- Si k = 1 no sabemos (Continuar)
- Funciona con : ( )n , ( )p(n)
- Si k < 1 la serie converge (Fin)
- Si k > 1 la serie diverge (Fin)
- Si k = 1 no sabemos (Continuar)
- Funciona con: kn , n ! , Semifactoriales ( 1·3·5 · · · · · (2n+1))
4.3 Serie de potencias
Una serie de potencias alrededor de x=0 es una serie de la forma:
Una serie de potencias alrededor de x=c es una serie de la forma:
En el cual el centro es c, y los coeficientes 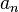 son los términos de una sucesion.
son los términos de una sucesion.
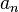 son los términos de una sucesion.
son los términos de una sucesion.4.4 Radio de convergencia
El radio de convergencia de una serie de la forma 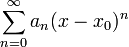 , con
, con 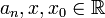 , viene dado por la expresión:
, viene dado por la expresión:
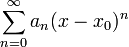 , con
, con 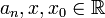 , viene dado por la expresión:
, viene dado por la expresión:
Si nos limitamos al conjunto de los números reales, una serie de la forma 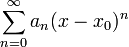 , con
, con 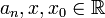 , recibe el nombre de serie de potencias centrada en
, recibe el nombre de serie de potencias centrada en 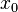 . La serie converge absolutamente para un conjunto de valores de
. La serie converge absolutamente para un conjunto de valores de  que verifica que
que verifica que 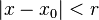 , donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de
, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de  pertenecientes al intervalo
pertenecientes al intervalo 
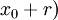 ,
ya que la convergencia para los extremos de este ha de estudiarse
aparte, por lo que el intervalo real de convergencia puede ser también
semiabierto o cerrado. Si la serie converge solo para
,
ya que la convergencia para los extremos de este ha de estudiarse
aparte, por lo que el intervalo real de convergencia puede ser también
semiabierto o cerrado. Si la serie converge solo para 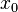 ,
, 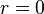 . Si lo hace para cualquier valor de
. Si lo hace para cualquier valor de  ,
, 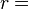

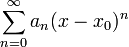 , con
, con 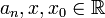 , recibe el nombre de serie de potencias centrada en
, recibe el nombre de serie de potencias centrada en 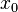 . La serie converge absolutamente para un conjunto de valores de
. La serie converge absolutamente para un conjunto de valores de  que verifica que
que verifica que 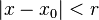 , donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de
, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de  pertenecientes al intervalo
pertenecientes al intervalo 
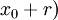 ,
ya que la convergencia para los extremos de este ha de estudiarse
aparte, por lo que el intervalo real de convergencia puede ser también
semiabierto o cerrado. Si la serie converge solo para
,
ya que la convergencia para los extremos de este ha de estudiarse
aparte, por lo que el intervalo real de convergencia puede ser también
semiabierto o cerrado. Si la serie converge solo para 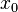 ,
, 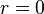 . Si lo hace para cualquier valor de
. Si lo hace para cualquier valor de  ,
, 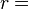

4.5 Serie de Taylor
En matemáticas, una serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto (a-r, a+r) se define como la siguiente suma:
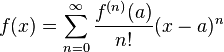
Aquí, n! es el factorial de n y f (n)(a) indica la n-ésima derivada de f en el punto a.
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor.
Una función es analítica si y solo si se puede representar con una
serie de potencias; los coeficientes de esa serie son necesariamente los
determinados en la fórmula de la serie de Taylor.
Si a = 0, a la serie se le llama serie de McLaurin.
Esta representación tiene tres ventajas importantes:
- La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
- Se puede utilizar para calcular valores aproximados de la función.
- Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.
Algunas funciones no se pueden escribir como serie de Taylor porque tienen alguna singularidad. En estos casos normalmente se puede conseguir un desarrollo en serie utilizando potencias negativas de x (véase Serie de Laurent. Por ejemplo f(x) = exp(−1/x²) se puede desarrollar como serie de Laurent
4.6 Representación de funciones mediante la serie de Taylor
En
matemáticas, una serie de Taylor de una función f(x) infinitamente
derivable (real o compleja) definida en un intervalo abierto (a-r, a+r)
se define como la siguiente suma:
Aquí, n! es el factorial de n y f (n)(a) indica la n-ésima derivada de f en el punto a.
Si
esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y
la suma es igual a f(x), entonces la función f(x) se llama analítica.
Para comprobar si la serie converge a f(x), se suele utilizar una
estimación del resto del teorema de Taylor. Una función es analítica si
y solo si se puede representar con una serie de potencias; los
coeficientes de esa serie son necesariamente los determinados en la
fórmula de la serie de Taylor.
Si a = 0, a la serie se le llama serie de Maclaurin
Esta representación tiene tres ventajas importantes:
* La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
* Se puede utilizar para calcular valores aproximados de la función.
*
Es posible demostrar que, si es viable la transformación de una función
a una serie de Taylor, es la óptima aproximación posible.
Algunas
funciones no se pueden escribir como serie de Taylor porque tienen
alguna singularidad. En estos casos normalmente se puede conseguir un
desarrollo en serie utilizando potencias negativas de x (véase Serie de
Laurent. Por ejemplo f(x) = exp(−1/x²) se puede desarrollar como serie
de Laurent. La serie de Taylor de una función f de números reales o
complejos que es infinitamente diferenciable en un entorno de números
reales o complejos a, es la serie de potencias:
que puede ser escrito de una manera más compacta como

4.7 Cálculo de Integrales de funciones expresadas como serie de Taylor
Este
teorema permite obtener aproximaciones polinómicas de una función en un
entorno de cierto punto en que la función sea diferenciable. Además el
teorema permite acotar el error obtenido mediante dicha estimación.
La
serie de Taylor de una funciónf de números reales o complejos que es
infinitamente diferenciable en un entorno de números reales o
complejosa, es la serie de potencias:
O en forma compacta:
que
puede ser escrito de una manera más compacta como donde n! es el
factorial de n yf(n)(a) denota la n-ésima derivada de f en el punto a;
la derivada cero de f es definida como la propia fy(x− a)0 y 0! son
ambos definidos como uno.
CASO DE UNA VARIABLE
Este
teorema permite aproximar una función derivable en el entorno reducido
alrededor de un punto a: E (a, d) mediante un polinomio cuyos
coeficientes dependen de las derivadas de la función en ese punto. Más
formalmente, si n ≥ 0 es un entero y  una función que es derivable n veces en el intervalo cerrado [a, x] y n +1 veces en el intervalo abierto (a, x).
una función que es derivable n veces en el intervalo cerrado [a, x] y n +1 veces en el intervalo abierto (a, x).
Donde  denota el factorial de
denota el factorial de  , y
, y  es el resto, término que depende de "x" y es pequeño si x está próximo al punto
es el resto, término que depende de "x" y es pequeño si x está próximo al punto  . Existen dos expresiones para
. Existen dos expresiones para  que se mencionan a continuación:
que se mencionan a continuación:
donde  y "x", pertenecen a los números reales,"n" a los enteros y
y "x", pertenecen a los números reales,"n" a los enteros y  es un número real entre
es un número real entre  y "x":
y "x":
Si  es expresado de la primera forma, se lo denomina Término complementario
de Lagrange, dado que el Teorema de Taylor se expone como una
generalización del Teorema del valor medio o Teorema de Lagrange,
mientras que la segunda expresión de R muestra al teorema como una
generalización del Teorema fundamental del cálculo integral.
es expresado de la primera forma, se lo denomina Término complementario
de Lagrange, dado que el Teorema de Taylor se expone como una
generalización del Teorema del valor medio o Teorema de Lagrange,
mientras que la segunda expresión de R muestra al teorema como una
generalización del Teorema fundamental del cálculo integral.
Para algunas funciones  , se puede probar que el resto,
, se puede probar que el resto,  , se aproxima a cero cuando se acerca al ∞; dichas funciones pueden
ser expresadas como series de Taylor en un entorno reducido alrededor
de un punto "a" y son denominadas funciones analíticas.
, se aproxima a cero cuando se acerca al ∞; dichas funciones pueden
ser expresadas como series de Taylor en un entorno reducido alrededor
de un punto "a" y son denominadas funciones analíticas.
El teorema de Taylor con  expresado de la segunda forma es también válido si la función
expresado de la segunda forma es también válido si la función  tiene números complejos o valores vectoriales. Además existe una
variación del teorema de Taylor para funciones con múltiples variables.
tiene números complejos o valores vectoriales. Además existe una
variación del teorema de Taylor para funciones con múltiples variables.
CASO DE VARIAS VARIABLES
El teorema de Taylor anterior puede generalizarse al caso de varias
variables como se explica a continuación. Sea B una bola en RN centrada en el punto a, y f una función real definida sobre la clausura  cuyas derivadas parciales de orden n+1 son todas continuas en cada
punto de la bola. El teorema de Taylor establece que para cualquier
cuyas derivadas parciales de orden n+1 son todas continuas en cada
punto de la bola. El teorema de Taylor establece que para cualquier  :
:
Donde
la suma se extiende sobre los multi-índices α (esta fórmula usa la
notación multi-índice). El resto satisface la desigualdad:
para
todo α con |α|=n+1. Tal como sucede en el caso de una variable, el
resto puede expresarse explícitamente en términos de derivadas
superiores
Ejemplo:
Ejemplo:
Suscribirse a:
Comentarios (Atom)