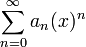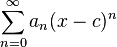CALCULO INTEGRAL

Unidad 4

Nombre de la asignatura: Cálculo Integral
Carrera: Ingeniería en Sistemas Computacionales
Clave de la asignatura: ACF-0902
(Créditos) SATCA: 3 - 2 - 5

TEMA: SERIES

4.1 Definición de serie.
4.1.1 Finita.
4.1.2 Infinita.
4.2 Serie numérica y convergencia Prueba de la razón (criterio de D´Alembert) y Prueba de la raíz (criterio de Cauchy).
4.3 Serie de potencias.
4.4 Radio de convergencia.
4.5 Serie de Taylor.
4.6 Representación de funciones mediante la serie de Taylor.
4.7 Cálculo de Integrales de funciones expresadas como serie de Taylor.

4.1 Definición de serie

Una serie es la suma indicada de los terminos de una sucesión.
Así, de las sucesiones anteriores obtenemos las series

1+4+9+16+25

Cuando el numero de terminos es limitado, se dice que la sucesion o serie es finita. Cuando el numero de terminos es ilimitado, la sucesición o serie se llama una sucesión infinita o una serie infinita.

El termino general o termino enesimo es una expresion que indica la ley de la fomación de los terminos

Ejemplo :

En la primera sucesión anterior, el termino general o termino enesimo es n². El primer terminose obtiene haciendo n=1, el decimo termino haciendo n=10

En matemáticas, una serie es la generalización de la noción de suma a los términos de una sucesión infinita. Informalmente, es el resultado de sumar los términos: a₁ + a₂ + a₃ + · · lo cual suele escribirse en forma más compacta con el símbolo de sumatorio:

$\sum a_n$ .

El estudio de las series consiste en la evaluación de la suma de un número finito n de términos sucesivos, y mediante un pasaje al límite identificar el comportamiento de la serie a medida que n crece indefinidamente.

Una secuencia o cadena «finita», tiene un primer y último término bien definidos; en cambio en una serie infinita, cada uno de los términos suele obtenerse a partir de una determinada regla o fórmula, o por algún algoritmo. Al tener infinitos términos, esta noción suele expresarse como serie infinita, pero a diferencia de las sumas finitas, las series infinitas requieren de herramientas del análisis matemático para ser debidamente comprendidas y manipuladas.

Existe una gran cantidad de métodos para determinar la naturaleza de convergencia o no-convergencia de las series matemáticas, sin realizar explícitamente los cálculos.

4.1.1 Finita.

Una serie numerica es un conjunto especial de números que se forma ordenadamente siguiendo determinada ley o condición, así por ejemplo.

2, 4, 6, 8, 10, 12, 14

2, 4, 8, 16, 32, 64,....

1, 1/2, 1/3, 1/4, 1/5

3, 6, 10, 12, 14, 20

Cuando la sucesión tiene un último término se dice que la sucesión es finita.

x i

= 0

para todo

i

>

n

y i

= 0

para todo

i

>

m

. En este caso el producto de

Cauchy de

Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.

x i = 0

para todo

i > n

y i = 0

para todo

i > m

En este caso el producto de Cauchy de $\sum x_i$ y $\sum y_i$ se verifica es $(x_0+\cdots + x_n)(y_0+\dots+y_m)$ .

Por lo tanto, para series finitas (que son sumas finitas), la multiplicación de Cauchy es directamente la multiplicación de las series.

4.1.2 Infinita.

Es un arrglo ordenado de numeros reales, uno para cada entero positivo. Mas formal mente una sucesión infinita es una funcion cuyo dominio es el conjunto de enteros positivos y cuyo rango es un conjunto de numeros reales. Podemos indicar una sucesion mediante a1 ,a2 ,a3,...., simplemete por {a_n}

Se puede especificar una sucesion dando suficientes terminos iniciales para establecer un patron como en

1, 4, 7, 10, 13, ....

mediante una formula explicita para el n-énesimo termino, como en

a_n = 3n-2, n ≥ 1

Para alguna $a,b\in\mathbb{R}$ , sea $x_n = a^n/n!\,$ y $y_n = b^n/n!\,$ . Entonces

$C(x,y)(n) = \sum_{i=0}^n\frac{a^i}{i!}\frac{b^{n-i}}{(n-i)!} = \frac{(a+b)^n}{n!}$

por definición y la fórmula binomial. Dado que, formalmente, 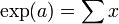$\exp(a) = \sum x$ y $\exp(b) = \sum y$ , se ha demostrado que $\exp(a+b) = \sum C(x,y)$ . Como el límite del producto de Cauchy de dos series absolutamente convergentes es igual al producto de los límites de esas series, se ha demostrado por lo tanto la fórmula

exp(a + b) = exp(a)exp(b)

para todo $a,b\in\mathbb{R}$ .

4.2 Serie numérica y convergencia Prueba de la razón (criterio de D´Alembert) y Prueba de la raíz (criterio de Cauchy).

Carácter de una serie.

Convergente: Cuando la suma es un número real.

Divergente: Cuando la suma da + o - infinito.

Oscilante: Cuando no es ninguna de las anteriores.

Convergencia de series con solo términos positivos

Teorema 1: Toda serie de términos positivos es convergente o divergente, pero nunca oscilante.

Teorema 2: Alterando arbitrariamente el orden de los términos, descomponiendo arbitrariamente cada uno de los sumandos, no se altera el carácter de la serie, ni varía su suma.

Criterio de Cauchy o de la Raíz. Calculamos :

Si k < 1 la serie converge (Fin)

Si k > 1 la serie diverge (Fin)

Si k = 1 no sabemos (Continuar)

Funciona con : ( )n , ( )p(n)

Criterio de D’Alembert o del cociente. Calculamos :

Si k < 1 la serie converge (Fin)

Si k > 1 la serie diverge (Fin)

Si k = 1 no sabemos (Continuar)

Funciona con: kn , n ! , Semifactoriales ( 1·3·5 · · · · · (2n+1))

4.3 Serie de potencias

Una serie de potencias alrededor de x=0 es una serie de la forma:

$\sum_{n=0}^\infty a_n (x)^n$

Una serie de potencias alrededor de x=c es una serie de la forma:

$\sum_{n=0}^\infty a_n (x-c)^n$

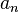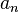En el cual el centro es c, y los coeficientes $a_n$ son los términos de una sucesion.

Hemos visto anteriormente los criterios de convergencia para series de números reales positivos o alternados. Utilizando toda esta riqueza analítica vamos a ocuparnos de investigar el comportamiento de una serie de funciones, en particular, de potencias, cuya convergencia va a depender del valor de la variable x. Es así como podremos introducir el concepto de radio de convergencia R. Dentro del intervalo (-R, R) la serie será convergente, fuera, divergente, y en los puntos de frontera, es decir, en x=-R e y=R, deberemos estudiar las series numéricas asociadas a estos dos puntos para determinar la convergencia o divergencia de la serie de potencias en ellos.

CALCULO INTEGRAL

martes, 10 de julio de 2012

Unidad 4

Temario Unidad 4

4.1 Definición de serie

4.1.1 Finita.

4.1.2 Infinita.

4.2 Serie numérica y convergencia Prueba de la razón (criterio de D´Alembert) y Prueba de la raíz (criterio de Cauchy).

4.3 Serie de potencias